Introduction
-
Definition (Gradient Flow in Linear Space)
X is a linear space, and $F:X \to \mathbb{R}$ is smooth. Gradient flow (or steepest descent curve) is a smooth curve $X:\mathbb{R}\to X$such that
$$
x'(t)=-\nabla F(x(t)).
$$
-
Existence and uniqueness of the solution
Since many PDEs are in the form of a gradient flow, the analysis can be applied to them.
Example
For $X=L^2(\mathbb{R}^n)$, a Hilbert space, and for Dirichlet energy $F(u)=\frac{1}{2}\int|\nabla u(x)|^2dx$, the Heat Equation $\partial_t u=\nabla^2u$ is a gradient flow problem.
-
Numerical methods and their convergence
Since gradient flow gradually minimizes $F(x)$, so many optimization methods are related to it, e.g. gradient descent, proximal descent methods, mirror descent.
-
Generalization to the gradient flow on general metric space
-
The need of viewing PDEs are gradient flows on general metric space, thus wider applicability.
Example
- PDEs in the continuity equation form $\partial_t-\nabla\cdot(\rho v)=0$, where $v=\nabla\frac{\delta F}{\delta \rho}$, can be cast as a gradient flow on the space of probabilities with Wasserstein distance.
- Heat Equation can also be viewed as gradient flow in the Wasserstein space.
-
The need of minimizing functionals on metric space.
Example
Optimization w.r.t. probability distributions, e.g. $\min_q KL(q||p)$. Optimization without parameterization is possible! (e.g. Stein Variational Gradient Descent)
-
Gradient Flow in the Euclidean Space
Variants of Gradient Flow in the Euclidean Space
Variant 1: $F$ is a convex and unnecessarily differentiable:
$$
\left\{\begin{aligned}x'(t)&\in -\partial F(x(t)), \quad a.e. t>0,\\x(0)&=x_0,\end{aligned}\right.
$$
where $x$ is an absolutely continuous curve, and
$$
\partial F(x)=\left\{ p\in\mathbb{R}^n:\forall y \in \mathbb{R}^n, F(y)\geq F(x)+p \cdot (y-x) \right\}.
$$
Theorem
Any two solutions $x_1,x_2$ of the above problem with different initial conditions satisfy $|x_1(t)-x_2(t)| \leq |x_1(0)-x_2(0)|$.
Corollary
For a given initial condition, the above problem has one unique solution.
Variant 2: $F$ is semi-convex ($\lambda$ convex)
Definition $\lambda$-convex function
$F$ is $\lambda$-convex $(\lambda\in \mathbb{R})$ if $F(x)-\frac{\lambda}{2}|x|^2$ is convex.
$$
\left\{\begin{aligned}x'(t)&\in -\partial F(x(t)), \quad a.e. t>0,\\x(0)&=x_0,\end{aligned}\right.
$$
where $x$ is an absolutely continuous curve, and
$$
\partial F(x)=\left\{ p\in\mathbb{R}^n:\forall y \in \mathbb{R}^n, F(y)\geq F(x)+p \cdot (y-x)+\frac{\lambda}{2}|y-x|^2 \right\}.
$$
Theorem
Any two solutions $x_1,x_2$ of the above problem with different initial conditions satisfy $|x_1(t)-x_2(t)|\leq e^{-\lambda t}|x_1(0)-x_2(0)|$.
Corollary
- For a given initial condition, the above problem has one unique solution.
- If $\lambda>0$ (strong convex), $F$ has a unique minimizer $x^*$. $x(t)\equiv x^*$ is a solution, so for any solution $x(t)$, $|x(t)-x^*|\leq e^{-\lambda t}|x(0)-x^*|$.
Approximating Curves
Definition (MMS)
Minimizing Movement Scheme (MMS): for a fixed small time step $\tau$, define a sequence $\left\{x_k^\tau\right\}_k$by
$$
x_{k+1}^{\tau}\in arg \min_x F(x)+\frac{|x-x_k^\tau|}{2\tau}.
$$
Importance:
- Practical numerical method for approximating the curve.
- Easier generalization to metric space, than $x'=-\nabla F(x)$ itself.
Properties:
- Existence of solution for mild F(e.g. Lipschitz and lower bounded by $C_1-C_2|x|^2$).
- $\frac{x_{k+1}^\tau-x_k^\tau}{\tau}\in -\partial F(x_{k+1}^\tau)$: implicit Euler scheme (more stable but hard than explicit one: gradient descent)
Convergence:
-
Define $v_{k+1}^\tau\triangleq\frac{x_{k+1}^\tau-x_k^\tau}{\tau}$, and $v^\tau(t)=v_{k+1}^\tau, t\in\left(k\tau,(k+1)\tau\right]$.
Define two kinds of interpolations:
- $x^\tau(t)=x_k^\tau, t\in\left(k\tau,(k+1)\tau\right]$;
- $\tilde{x}^\tau(t)=x_k^\tau+(t-k\tau)v_{k+1}\tau, t\in\left(k\tau,(k+1)\tau\right]$
$\tilde{x}^\tau$ is continuous and $(\tilde{x}^\tau)'=v^\tau$;
$x^\tau$ is not continuous, but $v^\tau(t)\in -\partial F(x^\tau(t))$.
Theorem
If $F(x_0)<+\infty$ and $\inf F>-\infty$, then up to a subsequence $\tau_j\to 0$, both $\tilde{x}^{\tau_j}$ and $x^{\tau_j}$ converge uniformly to a same curve $x\in H^1(\mathbb{R}^n)$ and $v^{\tau_j}$ weakly converges in $L^2(\mathbb{R};\mathbb{R}^2)$ to a vector function $v$ s.t. $x'=v$ and
- $v(t)\in\partial F(x(t))$ a.e., if $F$ is $\lambda$-convex;
- $v(t)=-\nabla F(x(t)). \forall t$. if $F$ is $C^1$.
Details:
-
$L^p$ space
-
For a measure space $(S,\sum,\mu)$, first define $\mathcal{L}(S;\mathbb{R}^n)\triangleq\left\{f:S\to \mathbb{R}^n\big|\int_S|f|^pd\mu < \infty\right\}$. It is a linear space.
-
Define $L^p(S;\mathbb{R}^n)\triangleq\mathcal{L}(S;\mathbb{R}^n)/\left\{f|f=0\quad \mu-a.e.\right\}$ to be a quotient space (i.e. treat all functions that are equal $\mu$-a.e.) as one same element in $L^p$).
Define $\|f\|_p\triangleq\left(\int_S|f|^pd\mu\right)^{1/p}$, then for $1\leq p\leq\infty$ it is a Banach space.
-
Only $L^2(S;\mathbb{R}^n)$ can be a Hilbert space, with inner product $\left<f,g\right>_{L^2(S;\mathbb{R}^n)}\triangleq\int_Sfg\;d\mu$.
-
$L^p(S)\triangleq L^p(S;\mathbb{R})$.
-
-
Weak convergence in a Hilbert space $\mathcal{H}$:
-
$x_n\in\mathcal{H}, n\geq 1, x\in\mathcal{H},x_n\rightharpoonup x$ is define as :
$\forall f\in\mathcal{H'},f(x_n)\to f(x).\Longleftrightarrow \forall y \in\mathcal{H},\left<x_n,y\right>_{\mathcal{H}}\to\left<x,y\right>_{\mathcal{H}}$.
-
$x_n\to x\Longrightarrow x_n\rightharpoonup x$.
$x_n\rightharpoonup x,\|x_n\|\to\|x\|\Longrightarrow x_n \to x$.
if $\dim(\mathbb{H})\leq\infty, x_n\rightharpoonup x\Longleftrightarrow x_n\to x$.
-
-
$H_k(\Omega)$ space $(\Omega \subset \mathbb{R}^n)$
-
Weak derivative. For $\mu \in C^k(\Omega)$ and $\phi \in C_c^{\infty}(\Omega)$ ($\cdot_c$ for compact support),
$$
\int_\Omega uD^{\alpha}\phi dx=(-1)^{|\alpha|}\int_{\Omega}\phi D^{\alpha}udx,(Integarl by parts)
$$
where $D^\alpha=\partial_{x_1}^{\alpha_1}\cdots\partial_{x_n}^{\alpha_n}$, and $|\alpha|=\sum_{i=1}^n\alpha_i$ is fixed as $k$. So define the weak $\alpha$-th partial derivative of $u$ as $v$:
$$
\int_\Omega uD^\alpha\phi dx=(-1)^\alpha\int_\Omega\phi vdx,\forall\phi\in C_{c}^{\infty}(\Omega).
$$
If it exists, it is uniquely defined a.e. -
Sobolev space $W^{k,p}(\Omega)$ for $k \in \mathbb{N}$ and $p\in[1,\infty]$:
$$
W^{k,p}(\Omega)=\left\{u\in L^P(\Omega):D^\alpha u\in L^p(\Omega),\forall |\alpha|\leq k\right\},
$$
with norm:
$$
\|u\|_{w^{k,p}(\Omega)}=\left\{\begin{aligned}&\left(\sum_{|\alpha|\leq k}\|D^\alpha u\|_{L^p(\Omega)}^p\right)^{\frac{1}{p}},\quad 1\leq p<+\infty,\\&\max_{|\alpha|\leq k}\|D^\alpha u\|_{L^\infty(\Omega)},\quad p=+\infty.\end{aligned}\right.
$$
$W^{k,p}(\Omega)$ is a Banach space. -
$H^k(\Omega)\triangleq W^{k,2}(\Omega)$. They are Hilbert space.
-
-
Up to a subsequence
There exists a sequence $\tau_j\to 0$ s.t. $\tilde{x}^{\tau_j}$ uniformly converge and $v^{\tau_j}$ weakly converge.
Characterizing Properties
Motivation
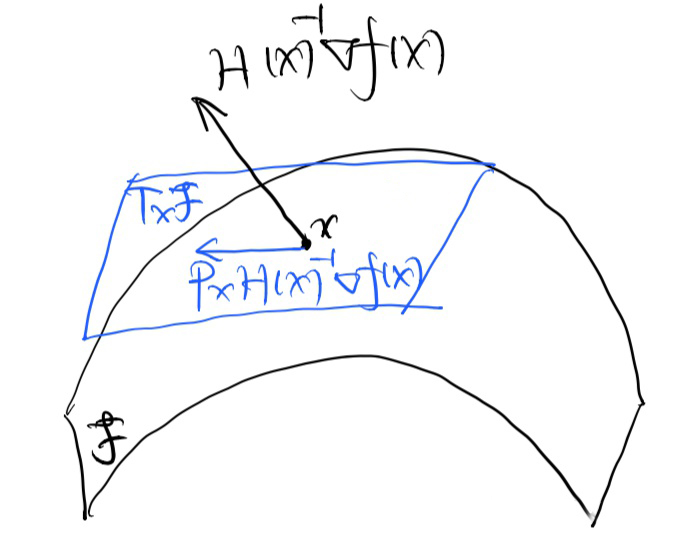
- $x'=-\nabla F(x)$ (or $x'\in -\partial F(x)$) is hard to generalize to metric space! There is nothing but distance in metric space, so $\nabla F(x)$ or $\partial F(x)$ cannot be defined! (different from manifold)
- Use two properties of gradient flow that can characterize it and can be generalized to metric space.
Two charactering properties of gradient flow in $\mathbb{R}^d$:
-
Energy Dissipation Equality (EDE) for $F\in C^1(\Omega)$, $\Omega\subset \mathbb{R}^n$:
$$
F(x(x))-F(x(t))=\int_s^t\left(\frac{1}{2}|x'(r)|^2+\frac{1}{2}|\nabla F(x(r))|^2\right)dr,\forall 0\leq s<t\leq 1
$$
is equivalent to $x'=-\nabla F(x)$. Note it is equivalent even for $"\geq"$(i.e $"\geq"\Longleftrightarrow "="$). -
Evolution Variational Inequality (EVI) for $\lambda$-convex function $F$:
$$
\frac{d}{dt}\frac{1}{2}|x(t)-y|^2\leq F(y)-F(x(t))-\frac{\lambda}{2}|x(t)-y|^2, \forall y\in X
$$
is equivalent to $x'(t)\in-\partial F(x(t))$.- Sometimes also denoted as $EVI_\lambda$.
- It is important for establishing the uniqueness and stability of gradient
flow.


0 条评论