简介
在工程应用中,我们经常会遇到下面的带限制的优化问题
$$
\begin{equation}\begin{aligned}\min_x \quad f(x), \\ s.t\quad Ax=b,x \in \bar{C}, \end{aligned}\end{equation}\tag{1.1}
$$
其中,$f$是一个函数,$A$为矩阵,$b$为列向量,$C$为一个开集合,$\bar{C}$为集合的$C$的闭包(可以理解为$C$的内部的点以及边界点组成的集合)。在$(1.1)$的问题中,我们需要找到一个$x$满足$Ax=b$,$x$在集合$\bar{C}$中,使得$f(x)$最小。
当没有限制的时候,即如果我们求解的问题是
$$
\begin{equation}\begin{aligned}\min_x f(x),\end{aligned}\end{equation} \tag{1.2}
$$
我们可以使用梯度下降算法来求解. 梯度下降在连续的情况下,即步长趋向于无限小的情况下,可以用常微分方程来表示,即
$$
\dot{x}(t)=-\nabla f(x(t))\tag{1.3}
$$
通过求解$(1.3)$我们得到了一个轨迹$x(t)$。当$t$增大的时候,$x(t)$逐渐趋向于函数$f$的最小值点。
现在,在我们要考虑的问题$(1.1)$中,我们对$x$的位置有了限制,因此,$(1.3)$中的梯度流的轨迹并不会总是满足$(1.1)$中的限制条件。因此,我们需要考虑其他办法。
论文《Hessian Riemannian gradient flows in convex programming》提出了梯度流$(1.3)$的一个变种来求解问题$(1.1)$。概括地说,该论文将$(1.1)$中的限制看成了一个流形(Manifold)。我们可以将该流形理解为满足中条件$(1.1)$的所有点构成的一个曲面。该论文作者构建了在该流形曲面上的梯度流,沿着该流形上的梯度流生成的轨迹一直待在曲面上,最后到达了$f$在该曲面上的最小值点。
接下来,我们介绍该论文的细节,并给出一个简单的例子。最后在总结中,我们指出该论文中的方法可以被拓展,用来求解带限制的单调算子(Monotone Operator)的求根问题。
海森黎曼梯度流
在这一节里,我们将叙述《Hessian Riemannian gradient flows in convex programming》这篇论文的主要思想。
如前所述,我们将问题$(1.1)$中的限制集合表示为一个流行(Manifold)。我们可以将流形想象为$n$维空间中的曲面,即$\mathbb{R}^n$空间中的一个子集。比如,整个$\mathbb{R}^n$可以看做一个流形,我们常见的球,轮胎,水杯等也可以看做一个流形。我们的目的就是要在这个流形上,找到一条轨迹,顺着这条轨迹,我们可以到达函数$f$在该流形上的最小值点。
首先,我们要研究限制集合组成的流形。我们知道集合$C$为$\mathbb{R}^n$空间中的开集。因此,集合$C$可以看作$\mathbb{R}^n$中的一个流形。如下图所示,曲线$\gamma$为流形$C$上的曲线,曲线依赖时间$t$,因此$\gamma$可以看作时间的一个函数。
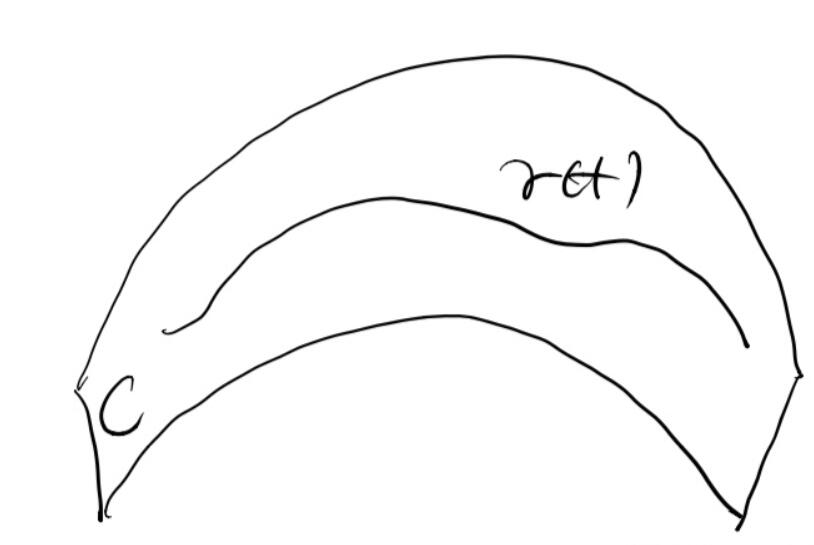
由微积分的知识,我们可知曲线$\gamma$在$[0,T]$的时间范围内的长度为
$$
\int_0^T|\dot{\gamma}(t)|dt,\tag{2.1}
$$
其中$\dot{\gamma}(t)$为$t$时刻$\gamma$的导数,几何意义上,$\dot{\gamma}(t)$为曲线在$\gamma(t)$这一点的切向量,如下图所示
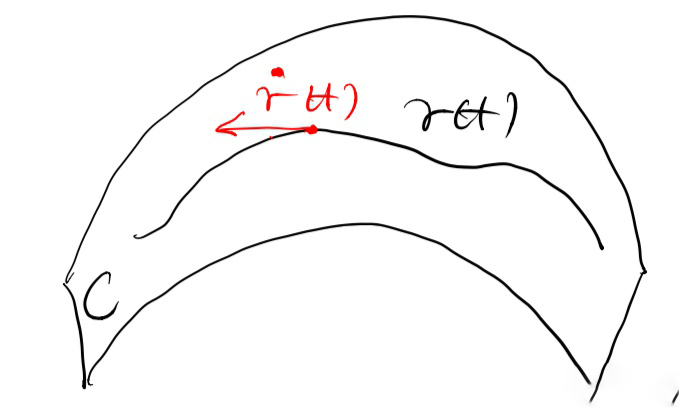
因此$|\dot{\gamma}(t)|$为该切向量的长度。等价的,我们可以将$(2.1)$写成下列形式
$$
\int_0^T\sqrt{\left<\dot{\gamma}(t),\dot{\gamma}(t)\right>}dt,\tag{2.2}
$$
其中,$\left<\cdot,\cdot\right>$表示两个向量的点积。我们将该点积称为测度(metric)。测度可以理解为某种测量工具,我们用测度来计算空间中某个曲线的长度,相当于我们拿带有某种刻度的直尺去量该曲线的长度。那么,如果我们的测量工具具有不同的单位,我们测出来的对象的长度的数值值也会不一样。相应地, 从$(2.2)$我们知道,如果我们改变测度的定义方式,那么我们就可以改变某条曲线的长度。例如,如果我们想让$\gamma$看起来是原来的$2$倍长度,那么我们可以将$4\left<\cdot,\cdot\right>$作为测度。
因此,在流形上,只要给我们一个测度,就相当于给了我们一把带有某种刻度测量工具,我们就可以用来在该流形的世界里上测量各种对象的几何属性,例如长度,体积等。数学上,测度计算的是流形上某一点处切平面上的两个向量的点积。如下图3所示,在流形$C$上某一点$x$处,我们考虑该点的切平面(即刚好挨着点$x$并与流形$C$相切的平面),记做$T_xC$。
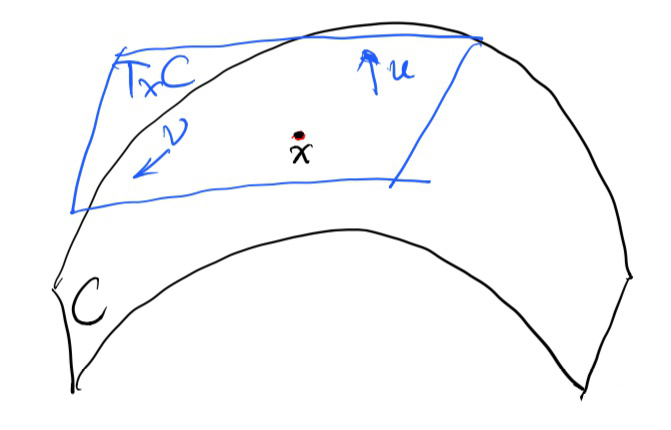
在$T_xC$上的两个向量$u,v$的点积即可被定义为
$$
g(u,v)=\left<u,v\right>\tag{2.3}
$$
回到我们需要考虑的限制集合$C$中,现在想象一个人走在该集合所在的曲面上。如何让人在该曲面上以一定的速率走(速度有限)而永远不离开该曲面呢?我们需要他要走的距离无限地远!即,我们需要曲面上任意一条到达曲面边界的曲线都无限长。为此,数学上,在流形$C$上,对于在某一点$x$处,切平面中任意两个向量$u,v$,的点积被计算为
$$
g(u,v)=\left<H(x)u,v\right>\tag{2.4}
$$
其中$H(x)$为正定可逆矩阵,当$x$靠近$C$的边界的时候,$H(x)$趋向于无穷大。所以,根据$(2.2)$的曲线长度的公式,如果某一条曲线到达了边界,那么这条曲线的长度为无穷大,所以沿着曲线以一定速度走,永远也不会达到边界。这样我们就解决了轨迹限制在集合$C$上的问题。
根据流形的理论,在$(2.4)$的测度定义下,函数$f$在流形$C$上的梯度为
$$
H(x)^{-1}\nabla f(x). \tag{2.5}
$$
接下来,我们考虑$(1.1)$中的线性限制。我们考虑集合$C$与集合$\left\{x|Ax=b\right\}$的交集。记$\mathcal{F}=C\cap\left\{x|Ax=b\right\}$。根据流形的理论,我们可得$\mathcal{F}$也是一个流形,并且是流形$C$的子流形。此时,在流形$\mathcal{F}$上,一个粒子沿着$(2.5)$的梯度指定的方向走,已经不能保证该粒子继续待在流形$\mathcal{F}$上了,我们必须把$(2.5)$定的梯度方向投影到粒子当前位置所在的切平面上,这样才能保证每次走依然是贴着流形$\mathcal{F}$在前进,如下图所示。
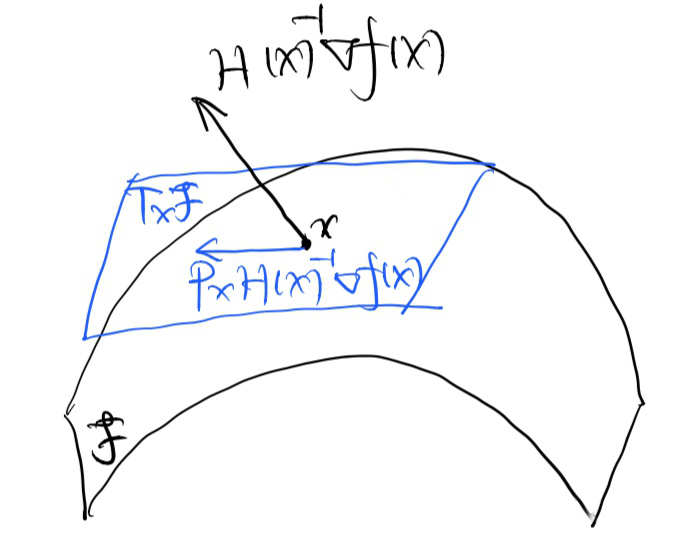
在线性限制的条件下,切平面即为集合$\left\{x|Ax=0 \right\}$,我们记$P_x$为将向量投影到点$x$处的切平面。因此,在$(2.4)$定义的测度下,$P_x$被计算为
$$
P_x=I-H(x)^{-1}A^T(AH(x)^{-1}A^T)^{-1}A.
$$
所以,在流形$\mathcal{F}$上,函数$f$的梯度为
$$
P_xH(x)^{-1}\nabla f(x).\tag{2.6}
$$
知道了在流形$\mathcal{F}$上的梯度,我们就可以在流形$\mathcal{F}$上定义像$(1.3)$一样的梯度流,我们有
$$
\left\{\begin{aligned}\dot{x}(t)&=-P_xH(x)^{-1}\nabla f(x),\\x(0)&\in\mathcal{F}.\end{aligned}\right.\tag{2.7}
$$
直觉上,$(2.7)$指的是,初始状态下,我们选取在流形$\mathcal{F}$上的一点,并从该点开始,沿着$f$在流形$\mathcal{F}$上的梯度的负方向走,最后到达$f$在流形上的最小值点。
例子
下面,我们来考虑一个简单的例子。我们做下列优化问题
$$
\left\{\begin{aligned}min_x\quad x,\\s.t. x\geq 0.\end{aligned}\right.\tag{3.1}
$$
这个例子,非常的简单,我们能直接看出最小值为$0$。下面我们使用前面所讲的海森黎曼梯度流来解决这个问题。首先,我们考虑梯度下降。这里,我们的的目标函数$f(x)=x$,因此,梯度为$1$。根据$(1.3)$,梯度流为
$$
\dot{x}(t)=-1.\tag{3.2}
$$
我们直接求解$(3.2)$,得到$x(t)=-t+x_0$,其中$x_0$为起始点。我么可以看出,当时间$t$超过一定的数值后,$x(t)$会变成负数,即离开$(3.1)$中$x\geq 0$的限制条件。这并不是我们需要的效果。
根据上面海森黎曼梯度流的知识,我们需要将$x>0$作为一个流形,并将梯度流的轨迹限制在$x>0$中。根据上一节的描述,我们要找到一个函数$H(x)$来定义$x>0$上的测度,并且$x$趋向于$x>0$的边界,即趋向于$x=0$的时候,$H(x)$趋向于无穷大。这里,我们选取
$$
H(x)=\frac{1}{x}.\tag{3.3}
$$
因此,根据$(2.5)$,函数$x$在新流形下的梯度为
$$
H(x)^{-1}\nabla x=x.\tag{3.4}
$$
所以,根据$(2.7)$,新的梯度流为
$$
\dot{x}(t)=-x(t).\tag{3.5}
$$
求解$(3.5)$,我们得到
$$
x(t)=x_0e^{-t}.\tag{3.6}
$$
从$(3.6)$,我们可以看出只要初始点$x_0$满足$x_0>0$那么整个轨迹$(3.6)$就停留在集合$x_0>0$中,当$t$趋向于无穷大时,$x(t)$趋向于$0$,即为我们需要求解的最小值点。并且,从$(3.6)$的公式可以看出,我们还有指数的衰减,即算法具有指数收敛性,收敛会相当快。
总结与拓展
本文我们介绍了海森黎曼梯度流的理论并给出了一个简单的事例。我们指出该论文中的方法可以被拓展,用来求解带限制的单调算子(Monotone Operator)的求根问题。在单调算子上的拓展可以用来在求解偏微分方程的时候保证某些量的正性,因为某些偏微分方程可以被离散为单调算子,从而能化解为单调算子的求根问题。具体地,单调算子$F$被定义为对于任意的$x$和$y$,$F$满足
$$
\left<F(x)-F(y),x-y\right>\geq 0.\tag{4.1}
$$
从$(4.1)$可以看出,单调算子是对单调增函数的推广。对于凸函数$f$来说,其梯度$\nabla f$即为单调算子。但相反地,并不是每一个单调算子都可以表示为一个凸函数的梯度。与梯度流$(1.3)$类似,我们可以构建单调流
$$
\dot{x}(t)=-F(x).\tag{4.2}
$$
我们期望在$(4.8)$的解存在的情况下,单调流会收敛到$F(x)=0$的解。相应地,对于带线性限制和开集限制的单调流,我们可以拓展海森黎曼梯度流,即将$(2.7)$拓展为
$$
\left\{\begin{aligned}\dot{x}(t)&=-P_xH(x)^{-1}F(x),\\x(0)&\in\mathcal{F}.\end{aligned}\right.
$$
关于使用单调流和海森黎曼单调流求解偏微分方程,可以参见论文《Two numerical approaches to stationary mean-field games》以及《The Hessian Riemannian flow and Newton's method for Effective Hamiltonians and Mather measures》。
转自https://zhuanlan.zhihu.com/p/344970146




0 条评论