重心坐标及其导数

数学中，重心坐标是由单形(如三角形或四面体等)顶点定义的坐标。重心坐标是齐次坐标的一种。

设$v_1, v_2, \cdots, v_n$ 是向量空间$V$中的一个单形的顶点，如果$V$中某点$p$满足
$$
(\lambda_1+\cdots+\lambda_n)p=\lambda_1v_1+\cdots+\lambda_nv_n
$$
那么我们称系数$(\lambda_1,\cdots,\lambda_n)$是$p$关于$v_1,v_2,\cdots,v_n$的重心坐标。这些顶点自己的坐标分别是$(1,0,0,\cdots,0), (0,1,0,0,\cdots,0) , \cdots, (0,0,0,\cdots,1)$重心坐标不是惟一的：对任何不等于零的$k$，$(k\lambda_1,\cdots,k\lambda_n)$也是$p$的重心坐标。但总可以取坐标满足$\lambda_1+\cdots+\lambda_n=1$，称为正规化坐标。注意到定义式在仿射变换下不变，故重心坐标具有仿射不变性。

如果坐标分量都非负，则$p$在$v_1,\cdots,v_n$的凸包内部，即由这些顶点组成的单形包含$p$。我们设想如果有质量$\lambda_1,\cdots,\lambda_n$分别位于单形的顶点，那么质量中心就是$p$。这是术语“重心”的起源，1827年由奥古斯特·费迪南德·莫比乌斯最初引入。

一维重心坐标

一维重心坐标求导

给定一个一维区间网格，计算每个单元上重心坐标函数的导数 区间单元$[x_0,x_1]$, 则对于任意的$x\in[x_0,x_1]$, 相应的定义在其重心坐标为$(\lambda_0,\lambda_1)$, 他们之间的关系如下
$$
\left[\begin{matrix}x_0 & x_1\\1 & 1\end{matrix}\right]\left[\begin{matrix}\lambda_0\\ \lambda_1\end{matrix}\right]=\left[\begin{matrix}x\\1\end{matrix}\right]
$$
即有
$$
\lambda_0=\frac{x_1-x}{x_1-x_0},\quad \lambda_1=\frac{x-x_0}{x_1-x_0}
$$
因此，重心坐标关于$x$的导数为
$$
\frac{d\lambda_0}{dx}=\frac{-1}{x_1-x_0},\quad \frac{d\lambda_1}{dx}=\frac{1}{x_1-x_0}
$$

一维重心坐标的物理意义

对任意的单元, 如图所示

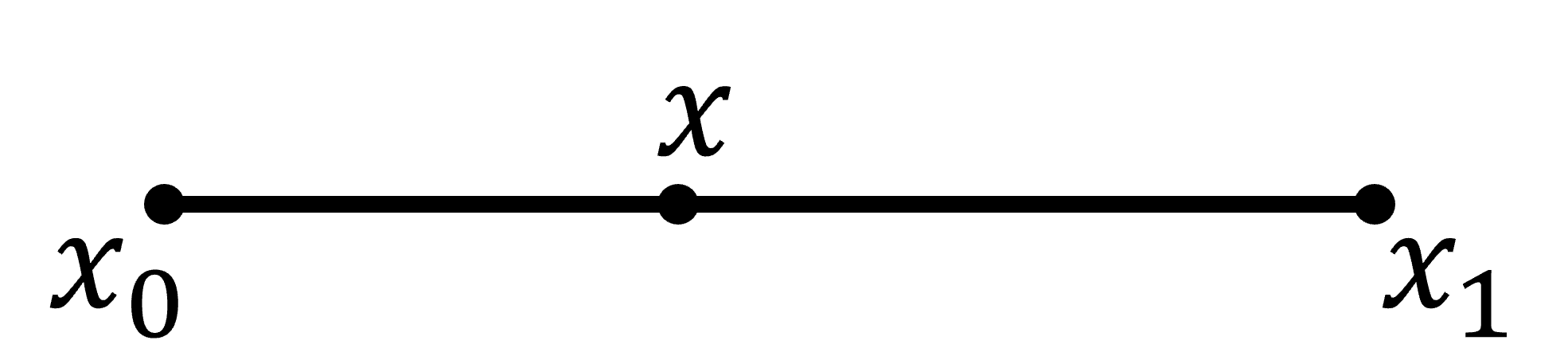
其上任意一点$x$的重心坐标为$\lambda_0,\lambda_1$，$\lambda_0$表示$x_0$所对的边$[x,x_1]$占整个区间$[x_0,x_1]$长度的比例，$\lambda_1$表示$x_1$所对应的边$[x_0,x]$占整个区间$[x_0,x_1]$​长度的比例。

import numpy as np
from fealpy.mesh import IntervalMesh
import matplotlib.pyplot as plt

node = np.array([[0.0], [0.5], [1.0]], dtype = np.float64)
cell = np.array([[0, 1], [1, 2]], dtype = np.int)
mesh = IntervalMesh(node, cell)
fig = plt.figure()
axes = fig.gca()
mesh.add_plot(axes)
mesh.find_node(axes, showindex = True)
mesh.find_cell(axes, showindex = True)
plt.show()

number_of_cells = mesh.number_of_cells()
node = mesh.entity('node')
cell = mesh.entity('cell')

length_of_cells = node[cell[:, 1], :] - node[cell[:, 0], :]
Dlambda = np.zeros((number_of_cells, 2, 1), dtype = np.float64)

Dlambda[:, 0, :] = -1 / length_of_cells
Dlambda[:, 1, :] = 1 / length_of_cells
print(Dlambda)

二维重心坐标

二维重心坐标函数求导

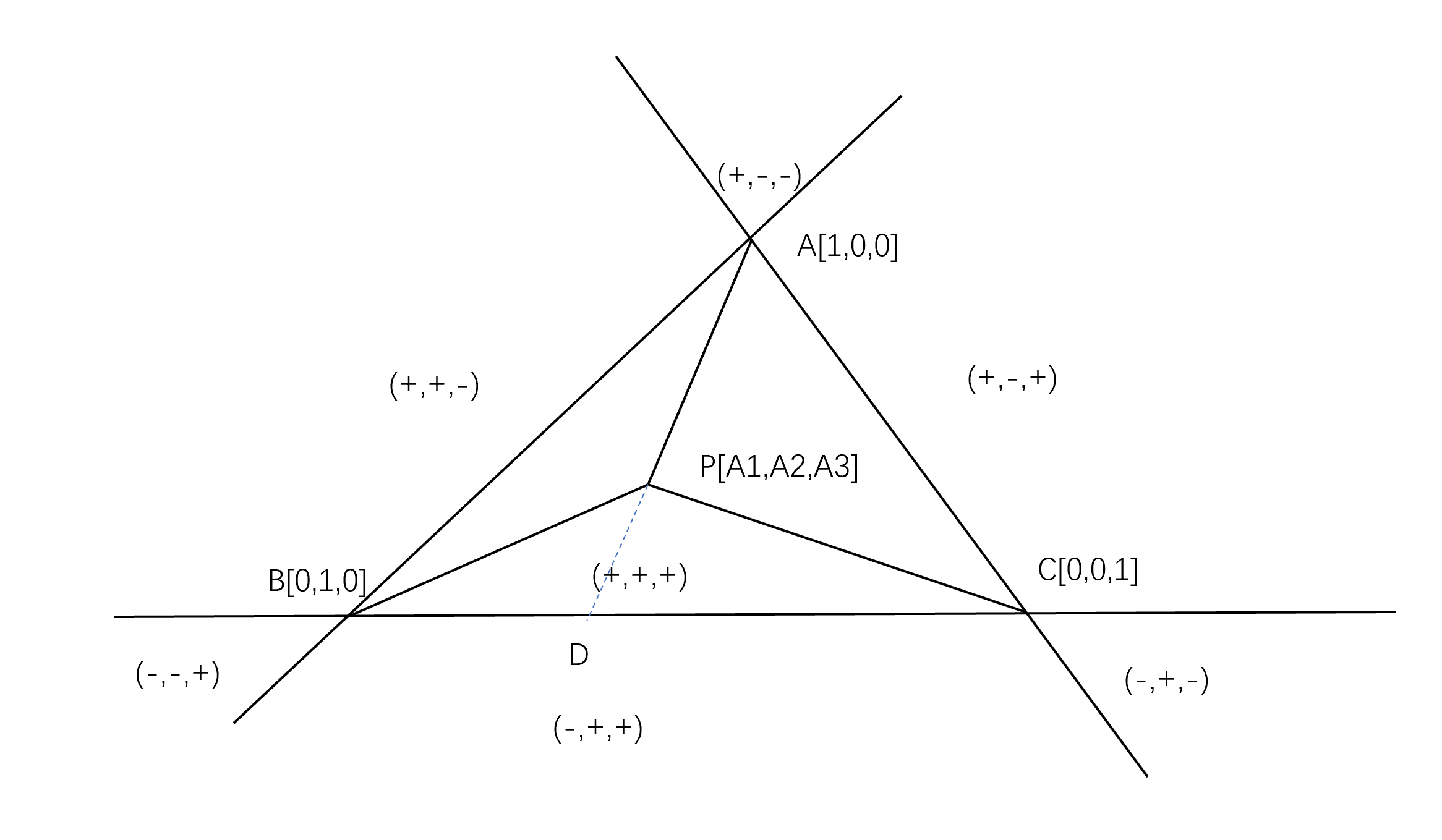
在三角形情形，重心坐标也叫面积坐$AP:PC$ 标，因为$p$点关于三角形 $ABC$的重心坐标和三角形 $PBC$, $PCA$ 及 $PAB$​ 的（有向）面积成比例，证明如下

设三角形$PBC,PCA$和$PAB$面积之比为$\lambda_0,\lambda_1,\lambda_2$且$\lambda_0+\lambda_1+\lambda_2=1$, 设射线$AP$与$BC$交于$D$,则$BD:DC=\lambda_1:\lambda_2$, 从而$d\frac{\lambda_1b+\lambda_2c}{\lambda_1+\lambda_2}$, $AP:PD=(\lambda_0+\lambda_1):\lambda_2$, 故$p=\frac{(\lambda_1+\lambda_2)d+\lambda_0a}{\lambda_0+\lambda_1+\lambda_2}$, $p=\lambda_0a+\lambda_1b+\lambda_2c$ 所以$(\lambda_0,\lambda_2,\lambda_3)$是$P$的重心坐标。

对于二维情况, 有对任意的一点$x=(x_0,x_1)^T$, 可以由三角形的三个顶点的凸组合表示, 记三角形的三个顶点分别为$x_i,i=0,1,2$。 则其重心坐标和点$x$之间的映射为
$$
A\lambda=X
$$
即
$$
\left[\begin{matrix}x_{00} & x_{10}& x_{20}\\x_{01}&x_{11}&x_{21}\\1&1 & 1\end{matrix}\right]\left[\begin{matrix}\lambda_0\\ \lambda_1\\\lambda_2\end{matrix}\right]=\left[\begin{matrix}x_0\\x_1\\1\end{matrix}\right]
$$
对上面的方程两边同乘以矩阵$A$​的逆可得
$$
A^{-1}=\left[\begin{matrix}a_{00}&a_{01}&a_{02}\\a_{10}&a_{11}&a_{12}\\a_{20}&a_{21}&a_{22}\end{matrix}\right]
$$
则有
$$
\left[\begin{matrix}\lambda_0\\ \lambda_1\\\lambda_2\end{matrix}\right]=\left[\begin{matrix}a_{00}&a_{01}&a_{02}\\a_{10}&a_{11}&a_{12}\\a_{20}&a_{21}&a_{22}\end{matrix}\right]\left[\begin{matrix}x_0\\x_1\\1\end{matrix}\right]
$$
由此就可以得到重心坐标函数的梯度为
$$
\nabla\lambda_0=\left[\begin{matrix}\frac{\partial\lambda_0}{\partial x_0}\\\frac{\partial\lambda_0}{\partial x_1}\\\end{matrix}\right]=\left[\begin{matrix}a_{00}\\a_{01}\end{matrix}\right]
$$

$$
\nabla\lambda_1=\left[\begin{matrix}\frac{\partial\lambda_1}{\partial x_0}\\\frac{\partial\lambda_1}{\partial x_1}\\\end{matrix}\right]=\left[\begin{matrix}a_{10}\\a_{11}\end{matrix}\right]
$$

$$
\nabla\lambda_2=\left[\begin{matrix}\frac{\partial\lambda_2}{\partial x_0}\\\frac{\partial\lambda_2}{\partial x_1}\\\end{matrix}\right]=\left[\begin{matrix}a_{20}\\a_{21}\end{matrix}\right]
$$

二维重心坐标的物理意义

对任意的单元, 如图所示

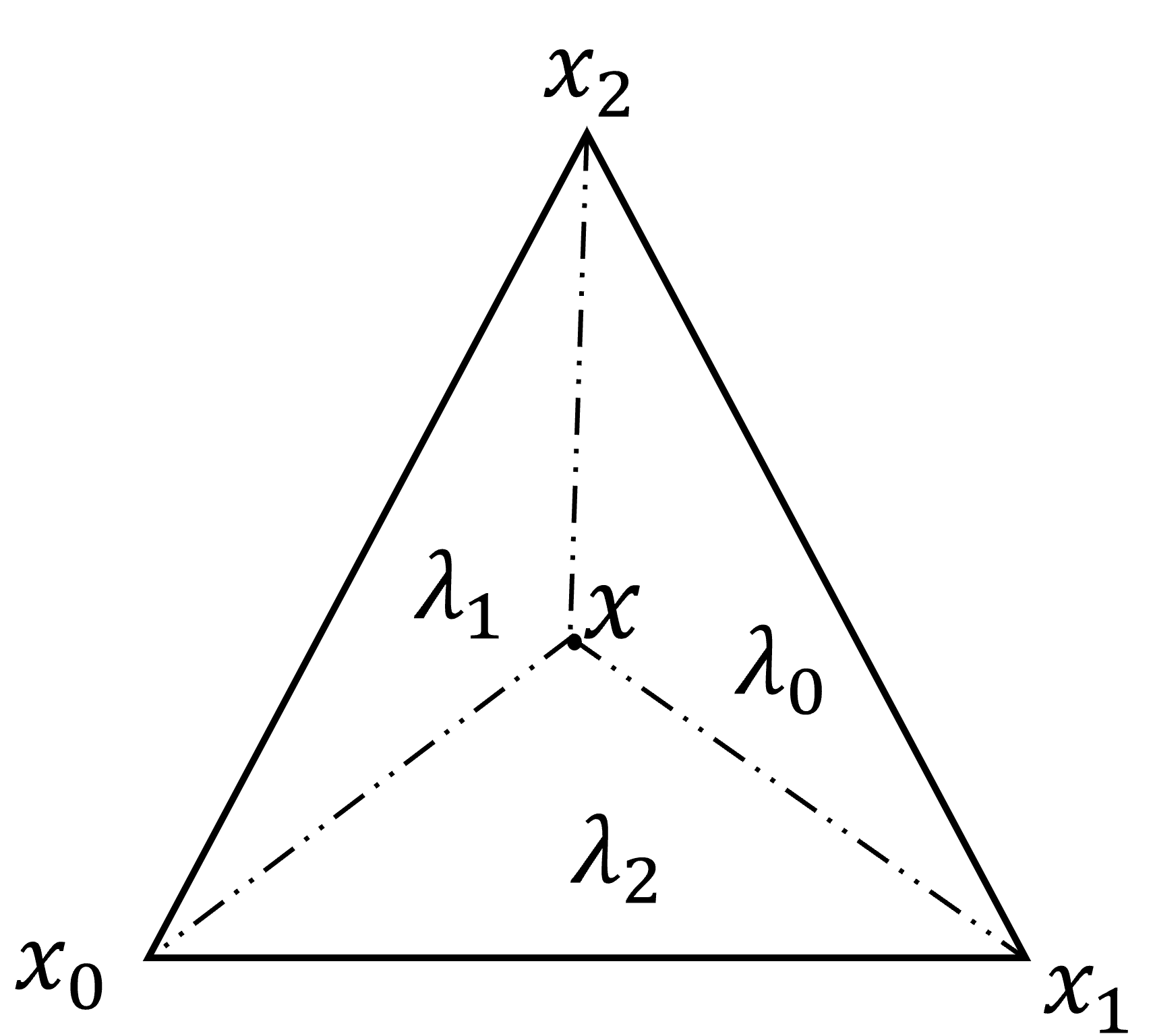
其上任意一点$x$的重心坐标为$\lambda_0,\lambda_1,\lambda_2$,

• $\lambda_0$表示$x_0$所对的三角形$\triangle_{x,x_1,x_2}$占整个三角形$\triangle_{x_0,x_1,x_2}$面积的比例。
• $\lambda_1$表示$x_1$所对的三角形$\triangle_{x,x_2,x_0}$占整个三角形$\triangle_{x_0,x_1,x_2}$面积的比例。
• $\lambda_0$表示$x_2$所对的三角形$\triangle_{x,x_0,x_1}$占整个三角形$\triangle_{x_0,x_1,x_2}$面积的比例。

而三角形的面积可由行列式计算得到, 由此就可以得到重心坐标的计算公式.

import numpy as np
from fealpy.mesh import MeshFactory as MF

box = [0, 1, 0, 1]
mesh = MF.boxmesh2d(box, nx = 1, ny = 1, meshtype = 'tri')
number_of_cells = mesh.number_of_cells()

import matplotlib.pyplot as plt
fig = plt.figure()
axes = fig.gca()
mesh.add_plot(axes)
mesh.find_node(axes, showindex = True)
mesh.find_cell(axes, showindex = True)
plt.show()

node = mesh.entity('node')
cells = mesh.entity('cell')
# print(cells.shape)

i = 0
Dlambda = np.zeros((number_of_cells, 3, 2), dtype=float)
for cell in cells:
    # print(cell)
    transform_matrix_A = np.array([node[cell, 0], node[cell, 1], np.ones((3), dtype = np.float64)], dtype = np.float64)
    # print(transform_matrix_A)
    inv_A = np.linalg.inv(transform_matrix_A)
    Dlambda[i, 0, :] = np.array([inv_A[0, 0], inv_A[0, 1]], dtype = float)
    Dlambda[i, 1, :] = np.array([inv_A[1, 0], inv_A[1, 1]], dtype = float)
    Dlambda[i, 2, :] = np.array([inv_A[2, 0], inv_A[2, 1]], dtype = float)
    i += 1
    # print(i, " cell:\n", transform_matrix_A)
    # print(inv_A)
print(Dlambda)

向量化编程

下面使用向量化编程重新进行计算，可以看到向量化运算大大提高了程序的计算速度

import numpy as np
from fealpy.mesh import MeshFactory as MF
import matplotlib.pyplot as plt

box = [0, 1, 0, 1]
mesh = MF.boxmesh2d(box, nx = 1, ny = 1, meshtype = 'tri')

number_of_cells = mesh.number_of_cells()
node = mesh.entity('node')
cells = mesh.entity('cell')

cells_A = np.zeros((3, 3, number_of_cells), dtype = float)
inv_cells_A = np.zeros((3, 3, number_of_cells), dtype = float)
cells_A[:, :, 0: number_of_cells] = np.array([node[cells[0: number_of_cells], 0].T, node[cells[0: number_of_cells], 1].T, np.ones_like(node[cells[0: number_of_cells], 0], dtype = float).T], dtype = float)
inv_cells_A = np.array([np.linalg.inv(cells_A[:, :, i]) for i in range(number_of_cells)], dtype = float)
Dlambda = inv_cells_A[:, :, 0: 2]
print(Dlambda)


# NC = mesh.number_of_cells()
# node = mesh.entity('node')
# cell = mesh.entity('cell')
# v0 = node[cell[:, 2], :] - node[cell[:, 1], :] # x 2 − x 1
# v1 = node[cell[:, 0], :] - node[cell[:, 2], :] # x 0 − x 2
# v2 = node[cell[:, 1], :] - node[cell[:, 0], :] # x 1 − x 0
# nv = np.cross(v2, -v1)

# Dlambda = np.zeros((NC, 3, 2), dtype=np.float64)
# length = nv #
# W = np.array([[0, 1], [-1, 0]], dtype=np.int_)
# Dlambda[:,0,:] = v0@W/length.reshape(-1, 1)
# Dlambda[:,1,:] = v1@W/length.reshape(-1, 1)
# Dlambda[:,2,:] = v2@W/length.reshape(-1, 1)
# print(Dlambda)

三维重心坐标函数

三维重心坐标函数求导

对于三维情况, 有对任意的一点$x=(x_0,x_1,x_2)^T$​, 可以由三角形的三个顶点的凸组合表示, 记三角形的三个顶点分别为$x_i,i=0,1,2,3$。 则其重心坐标和点$x$之间的映射为
$$
A\lambda=X
$$
即
$$
\left[\begin{matrix}x_{00} & x_{10}& x_{20}& x_{30}\\x_{01}&x_{11}&x_{21}& x_{31}\\x_{02}&x_{12}&x_{22}&x_{32}\\1&1 & 1&1\end{matrix}\right]\left[\begin{matrix}\lambda_0\\ \lambda_1\\\lambda_2\\\lambda_3\end{matrix}\right]=\left[\begin{matrix}x_0\\x_1\\x_2\\1\end{matrix}\right]
$$
对上面的方程两边同乘以矩阵A的逆可得
$$
\lambda=A^{-1}x
$$
记矩阵$A^{-1}$中的元素为
$$
A^{-1}=\left[\begin{matrix}a_{00}&a_{01}&a_{02}&a_{03}\\a_{10}&a_{11}&a_{12}&a_{13}\\a_{20}&a_{21}&a_{22}&a_{23}\\a_{30}&a_{31}&a_{32}&a_{33}\end{matrix}\right]
$$
则有
$$
\left[\begin{matrix}\lambda_0\\ \lambda_1\\\lambda_2\\\lambda_3\end{matrix}\right]=\left[\begin{matrix}a_{00}&a_{01}&a_{02}&a_{03}\\a_{10}&a_{11}&a_{12}&a_{13}\\a_{20}&a_{21}&a_{22}&a_{23}\\a_{30}&a_{31}&a_{32}&a_{33}\end{matrix}\right]\left[\begin{matrix}x_0\\x_1\\x_2\\1\end{matrix}\right]
$$
由此就可以得到重心坐标函数的梯度为
$$
\nabla\lambda_0=\left[\begin{matrix}\frac{\partial\lambda_0}{\partial x_0}\\\frac{\partial\lambda_0}{\partial x_1}\\\frac{\partial\lambda_0}{\partial x_2}\\\end{matrix}\right]=\left[\begin{matrix}a_{00}\\a_{01}\\a_{02}\end{matrix}\right]
$$

$$
\nabla\lambda_1=\left[\begin{matrix}\frac{\partial\lambda_1}{\partial x_0}\\\frac{\partial\lambda_1}{\partial x_1}\\\frac{\partial\lambda_1}{\partial x_2}\\\end{matrix}\right]=\left[\begin{matrix}a_{10}\\a_{11}\\a_{12}\end{matrix}\right]
$$

$$
\nabla\lambda_2=\left[\begin{matrix}\frac{\partial\lambda_2}{\partial x_0}\\\frac{\partial\lambda_2}{\partial x_1}\\\frac{\partial\lambda_2}{\partial x_2}\\\end{matrix}\right]=\left[\begin{matrix}a_{20}\\a_{21}\\a_{22}\end{matrix}\right]
$$

$$
\nabla\lambda_3=\left[\begin{matrix}\frac{\partial\lambda_3}{\partial x_0}\\\frac{\partial\lambda_3}{\partial x_1}\\\frac{\partial\lambda_3}{\partial x_2}\\\end{matrix}\right]=\left[\begin{matrix}a_{30}\\a_{31}\\a_{32}\end{matrix}\right]
$$

三维重心坐标的物理意义

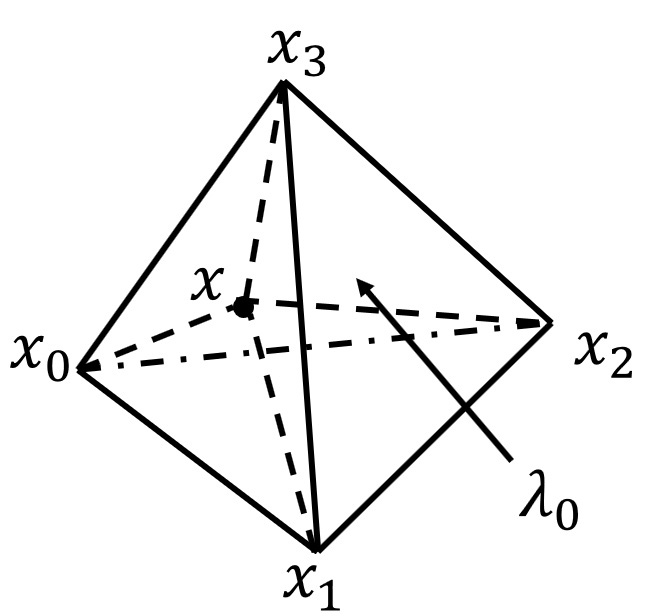
其上任意一点$x$的重心坐标为$\lambda_0,\lambda_1,\lambda_2,\lambda_3$,

• $\lambda_0$表示$x_0$所对的四面体$\triangle_{x,x_1,x_2,x_3}$占整个四面体$\triangle_{x_0,x_1,x_2，x_3}$体积的比例。
• $\lambda_1$表示$x_1$所对的四面体$\triangle_{x,x_0,x_2,x_3}$占整个四面体$\triangle_{x_0,x_1,x_2，x_3}$体积的比例。
• $\lambda_2$表示$x_2$所对的四面体$\triangle_{x,x_0,x_1,x_3}$占整个四面体$\triangle_{x_0,x_1,x_2，x_3}$体积的比例。
• $\lambda_3$表示$x_3$所对的四面体$\triangle_{x,x_0,x_1,x_2}$占整个四面体$\triangle_{x_0,x_1,x_2，x_3}$体积的比例。

而四面体的体积可由行列式计算得到, 同样可以得到重心坐标的计算公式。

import numpy as np
from fealpy.mesh import MeshFactory as MF
import matplotlib.pyplot as plt

mesh = MF.one_tetrahedron_mesh(meshtype = 'iso')
number_of_cells = mesh.number_of_cells()

fig = plt.figure()
axes = fig.gca(projection='3d')
mesh.add_plot(axes)
mesh.find_node(axes, showindex=True)
mesh.find_cell(axes, showindex=True)
plt.show()

node = mesh.entity('node')
cells = mesh.entity('cell')
print(cells.shape)

i = 0
Dlambda = np.zeros((number_of_cells, 4, 3), dtype=float)
for cell in cells:
    print(cell)
    transform_matrix_A = np.array([node[cell, 0], node[cell, 1], node[cell, 2], np.ones((4), dtype = np.float64)], dtype = np.float64)
    inv_A = np.linalg.inv(transform_matrix_A)
    Dlambda[i, 0, :] = np.array([inv_A[0, 0], inv_A[0, 1], inv_A[0, 2]], dtype = float)
    Dlambda[i, 1, :] = np.array([inv_A[1, 0], inv_A[1, 1], inv_A[1, 2]], dtype = float)
    Dlambda[i, 2, :] = np.array([inv_A[2, 0], inv_A[2, 1], inv_A[2, 2]], dtype = float)
    Dlambda[i, 3, :] = np.array([inv_A[3, 0], inv_A[3, 1], inv_A[3, 2]], dtype = float)
    i += 1
    # print(i, " cell:\n", transform_matrix_A)
    # print(inv_A)
print(Dlambda)

向量化编程

下面使用向量化编程重新进行计算，可以看到向量化运算大大提高了程序的计算速度

import numpy as np
from fealpy.mesh import MeshFactory as MF
import matplotlib.pyplot as plt

mesh = MF.one_tetrahedron_mesh(meshtype = 'iso')
number_of_cells = mesh.number_of_cells()

fig = plt.figure()
axes = fig.gca(projection='3d')
mesh.add_plot(axes)
mesh.find_node(axes, showindex=True)
mesh.find_cell(axes, showindex=True)
plt.show()

node = mesh.entity('node')
cells = mesh.entity('cell')
print(cells.shape)

cells_A = np.zeros((4, 4, number_of_cells), dtype = float)
inv_cells_A = np.zeros((4, 4, number_of_cells), dtype = float)
cells_A[:, :, 0: number_of_cells] = np.array([node[cells[0: number_of_cells], 0].T, node[cells[0: number_of_cells], 1].T, node[cells[0: number_of_cells], 2].T, np.ones_like(node[cells[0: number_of_cells], 0], dtype = float).T], dtype = float)
inv_cells_A = np.array([np.linalg.inv(cells_A[:, :, i]) for i in range(number_of_cells)], dtype = float)
Dlambda = inv_cells_A[:, :, 0: 3]
print(Dlambda)