快速傅里叶变换

准备

FT (Fourier Transform): 傅里叶变换

DFT (Discrete Fourier Transform): 离散傅里叶变换

FFT (Fast Fourier Transform): 快速傅里叶变换

IFFT (Inverse Fourier Transform): 快速傅里叶变换逆变换

旋转因子：$W_{N}^{kn}=e^{-j\frac{2\pi}{N}kn}$

多项式的系数表示法

形如$a_0+a_1x+a_2x^2+\cdots+a_nx^n$的代数表达式，是以系数形式表示的，将$n$次多项式$A(x)$的系数$a_0,a_1,\cdots,a_n$看作$n+1$维向量$\vec{a}=(a_0,a_1,\cdots,a_n)$, 其系数表示(coefficient representation)就是$\vec{a}$.

多项式的点值表示

如果选取$n+1$个不同的数$x_0,x_1,\cdots,x_n$对多项式进行求值, 得到$A(x_0),A(x_1),\cdots,A(x_n)$, 那么就称$(x_i,A(x_i)):0\leq i\leq n,i \in\mathbb{Z}$为多项式$A(x)$的点值表示(point-value representation)

多项式$A(x)$的点值表示不止一种,你只要选择不同的数就可以得到不同的点值表示, 但是任何一种点值表示都能唯一确定一个多项式, 为了从点值表示转换成系数表示, 可以直接通过插值的方式.
$$
\left[\begin{matrix}A(x_0)\\A(x_1)\\ \vdots\\A(x_n)\end{matrix}\right]=\left[\begin{matrix}1&x_0&x_0^2&\cdots&x_0^{n}\\1&x_1&x_1^2&\cdots&x_1^n\\&&\vdots&&\\1&x_n&x_n^2&\cdots&x_n^n\end{matrix}\right]\left[\begin{matrix}a_0\\a_1\\\vdots \\a_n\end{matrix}\right]
$$
有Vandermonde determinant保证系数唯一性

快速傅里叶变换

快速傅里叶变换你可以认为有两个部分，DFT 和 IDFT，分别可以在$\mathcal{O}(n\log{n})$的时间内将多项式的系数表示转化成点值表示，并且转回来，就像下面这张图所示：

单位根

单位根所在的点是把单位圆（以原点为圆心，半径为1的圆）从（0,1）开始平均分成n份的分割点
这就是n=8时的单位圆，绿色圆上的红点就是单位根所在的点

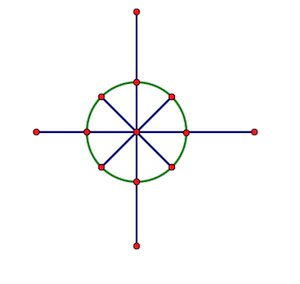
在复数范围内令$\omega^n=1$可以得到n个不同的复数根$\omega_n^0,\omega_n^1,\cdots,\omega_n^{n-1}$且均匀分布在模长为1的圆上, $\omega_n^1$被称为$n$次单位圆根. 每个单位根即
$$
\omega_n^k=(\cos{\frac{k}{n}2\pi},\sin{\frac{k}{n}2\pi})
$$

性质1:$\omega_n^k=(\omega_n^1)^k$
$$
\begin{aligned}\omega_n^k\times\omega_n^1=&(\cos{\frac{k}{n}2\pi},\sin{\frac{k}{n}2\pi})*(\cos{\frac{1}{n}2\pi},\sin{\frac{1}{n}2\pi})\\=&(\cos{\frac{k}{n}2\pi}*\cos{\frac{1}{n}2\pi}-\sin{\frac{k}{n}2\pi}*\sin{\frac{1}{n}2\pi},\sin{\frac{k}{n}2\pi}*\cos{\frac{1}{n}2\pi}+\cos{\frac{k}{n}2\pi}*\sin{\frac{1}{n}2\pi})\\=&(\cos{\frac{k+1}{n}2\pi},\sin{\frac{k+1}{n}2\pi})\\=&\omega_n^{k+1}\end{aligned}
$$
推论: $(\omega_n^x)^y=((\omega_n^1)^x)^y=(\omega_n^1)^{x*y}=\omega_n^{x*y}$

性质2: 对于任意一个正整数$x$, $\omega_{n*k}^{k*x}=\omega_n^k$

$$
\begin{aligned}\omega_{n*x}^{k*x}=&(\cos{\frac{k*x}{n*x}2\pi},\sin{\frac{k*x}{n*x}2\pi})\\=&(\cos{\frac{k}{n}2\pi},\sin{\frac{k}{n}2\pi})\\=&\omega_n^k\end{aligned}
$$
性质3:如果$n$是偶数, 那么$\omega_n^{k+\frac{n}{2}}=-\omega_n^k$
$$
\begin{aligned}\omega_n^{k+\frac{n}{2}}=&(\cos{\frac{k+\frac{n}{2}}{n}}2\pi,\sin{\frac{k+\frac{n}{2}}{n}2\pi})\\=&(-\cos{\frac{k}{n}2\pi},-\sin{\frac{k}{n}2\pi})\\=&-(cos{\frac{k}{n}2\pi},sin{\frac{k}{n}2\pi})\\=&-\omega_n^k\end{aligned}
$$
$$\omega_{\frac{n}{m}}^{k}=\omega_n^{mk}$$

$$\sum_{k=0}^{n-1}(\omega_n^{j-i})^k=\left\{\begin{aligned}0,\;i\neq j\\n,\;i=j\end{aligned}\right.$$

带入单位根带来的性质, 离散傅里叶变换，它是求值的时候把x的值分别取$\omega_n^0,\omega_n^1,\cdots,\omega_n^{n-1}$这$n$个数, 能够方便的实现插值, 插值是暴力算法的瓶颈, 现在定义对函数$f(x)$的离散傅里叶变换为将$\omega_n^0,\omega_n^1,\cdots,\omega_n^{n-1}$这$n$个数作为$x_0,x_1,\cdots,x_{n-1}$带入, 离散傅里叶变换的结果为$(y_0,y_1,\cdots,y_{n-1})$, 容易发现, 这是一个插值过程. 然后有一个结论: 一个多项式$A(x)$在进行傅里叶变换后, 将离散傅里叶变换的结果的$n$个$y$作为系数组成多项式$B(x)$, 原来的$n$个单位根倒数进行求值, 结果的每个数除以$n$, 其结果就是$A(x)$的各项系数

$A(x)=a_0x^0+a_1x^1+\cdots+a_{n-1}x^{n-1}$将$\omega_n^0,\omega_n^1,\cdots,\omega_n^{n-1}$作为$x$分别带入求值得到$(y_0,y_1,\cdots,y_{n-1})$, 将这些$y$作为系数,产生一个新的多项式$B(x)=b_0x^0+b_1x^1+\cdots+b_{n-1}x^{n-1}$, 将$\omega_n^{-0},\omega_n^{-1},\cdots,\omega_n^{-(n-1)}$作为$x$分别带入求值得到的$(z_0,z_1,\cdots,z_{n-1})$对于每个$z_k$, 有$z_k=a_k*n$

$$
\begin{aligned}z_k=&\sum_{i=0}^{n-1}y_i*(\omega_n^{-k})^i\\=&\sum_{i=0}^{n-1}(\sum_{j=0}^{n-1}a_j*(\omega_n^i)^j)*(\omega_n^{-k})^i\\=&\sum_{i=0}^{n-1}\sum_{j=0}^{n-1}a_j*(\omega_n^i)^j*(\omega^{-k})^i\\=&\sum_{i=0}^{n-1}\sum_{j=0}^{n-1}a_j*\omega_n^{i*j}*\omega_n^{-k*i}\\=&\sum_{j=0}^{n-1}a_j\left(\sum_{i=0}^{n-1}(\omega_n^{j-k})^i\right)\end{aligned}
$$

然后对于$\sum_{i=0}^{n-1}(\omega_n^{j-k})^i$, 容易发现,

如果$j-k=0$那么$\omega_n^{j-k}$就是$\omega_n^0=1$, 所以$n$个$1$结果为$n$

如果$j-k\neq 0$那么通过等比数列求和$(x^0+x^1+\cdots,x^{n-1}=\frac{x^n-1}{x-1})$可以发现, 结果$\frac{(\omega_n^{j-k})^n-1}{\omega_n^{j-k}-1}=\frac{(\omega_n^n)^{j-k}-1}{\omega_n^{j-k}-1}=0$

所以说,这个系数只有在$j-k=0$,即$j=k$时, 才为$n$, 其他都为$0$, 所以$z_k=a_k*n$.

FFT

FFT如何减少计算量

简单来讲就是数学家利用上面提到的旋转因子W的周期性，对称性等性质进行公式化简。在算法编程中则是不断利用已经计算过的点来算新的点，即：旧点算新点。

注意：单纯地拆分多点序列为少点序列而没有进行化简是运算量并没有减少！拆分只是为化简服务，利用旋转因子进行化简才是运算量降低的关键！

蝶形运算

对于蝶形运算，可以理解为通过图形来定义的运算。左边是输入，右边是输出结果，对于横线上的字母有两种情况表示：

左端线上有数字表示(没有则表示C和D为1):

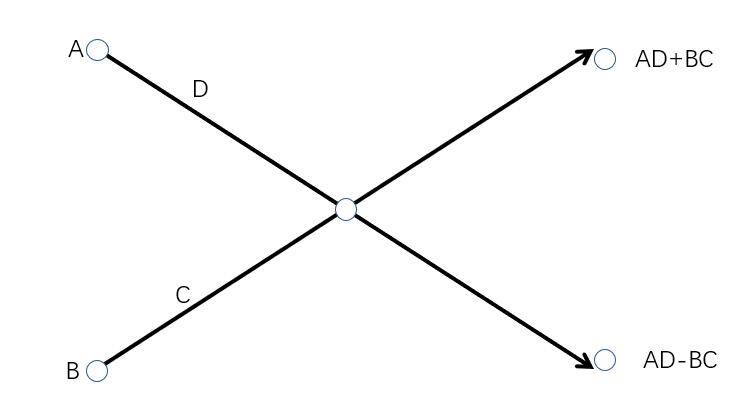
右端线上有数字表示(没有则表示C和D为1):

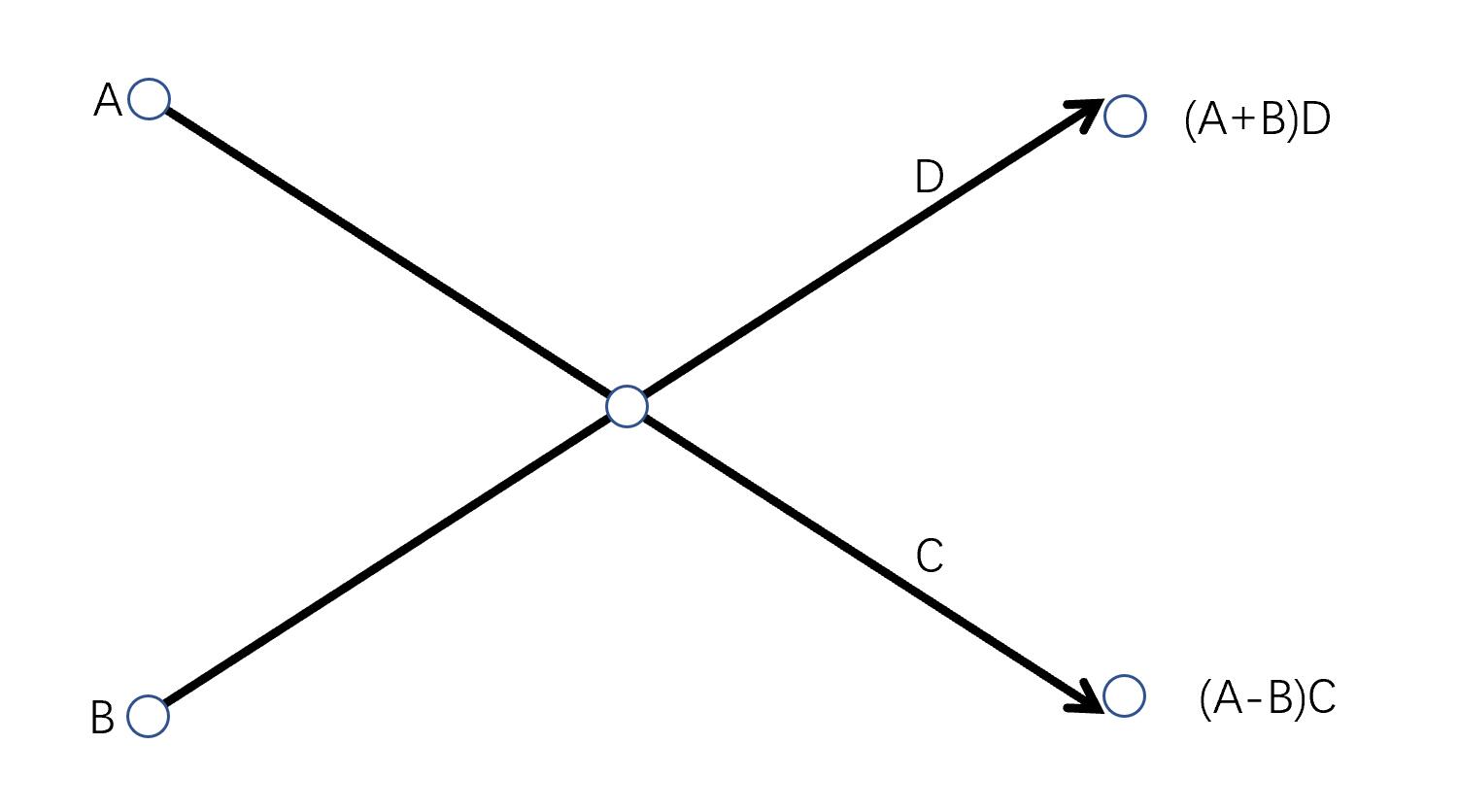
对于$A(x)=\sum_{i=0}^{n-1}a_ix_i=a_0+a_1x^1+a_2x^2+\cdots+a_{n-1}^{n-1}$

按$A(x)$下标奇偶性把$A(x)$分成两半，右边再提一个$x$：
$$
\begin{aligned}A(x)&=(a_0+a_2x^2+\cdots+a_{n-2}x^{n-2})+(a_1x^1+a_3x^3+\cdots+a_{n-1}x^{n-1})\\&=(a_0+a_2x^2+\cdots+a_{n-2}x^{n-2})+x(a_1+a_3x^2+\cdots+a_{n-1}x^{n-2})\end{aligned}
$$

这里默认$n$是$2^k(k\in N^+)$, 不然则可以对$n$进行扩展

令
$$
\begin{aligned}A_0(x)&=a_0+a_2x^1+\cdots+a_{n-2}x^{\frac{n}{2}-1}\\A_1(x)&=a_1+a_3x^1+\cdots+a_{n-1}x^{\frac{n}{2}-1}\end{aligned}
$$
所以有$A(x)=A_0(x^2)+xA_1(x^2)$, 对$A(x)$带入$\omega_n^m(m<\frac{n}{2})$有
$$
\begin{aligned}A(\omega_n^m)&=A_0((\omega_n^m)^2)+\omega_n^mA_1((\omega_n^m)^2)\\&=A_0(\omega_n^{2m})+\omega_n^mA_1(\omega_n^{2m})\\&=A_{0}(\omega_{\frac{n}{2}}^m)+\omega_n^mA_1(\omega_{\frac{n}{2}}^m)\end{aligned}
$$
再带入$\omega_n^{m+\frac{n}{2}}$:
$$
\begin{aligned}A(\omega_n^{m+\frac{n}{2}})&=A_0(\omega_n^{2m+n})+\omega_n^{m+\frac{n}{2}} A_1(\omega_n^{2m+n})\\&=A_0(\omega_n^{2m}\omega_n^n)-\omega_n^mA_1(\omega_n^{2m}\omega_n^n)\\&=A_0(\omega_\frac{n}{2}^m)-\omega_n^mA_1(\omega_\frac{n}{2}^{m})\end{aligned}
$$
综上
$$
\begin{aligned}A(\omega_n^m)&=A_0(\omega_\frac{n}{2}^m)+\omega_n^mA_1(\omega_\frac{n}{2}^m)\\A(\omega_n^{m+\frac{n}{2}})&=A_0(\omega_{\frac{n}{2}}^m)-\omega_n^mA_1(\omega_\frac{n}{2}^m)\end{aligned}
$$
带入单位根之后更清楚
$$
\begin{aligned}A(\omega^j)&=A_0(\omega^{2j})+\omega^jA_1(\omega^{2j})\\A(-\omega^j)&=A_0(\omega^{2j})-\omega^{j}A_1(\omega^{2j})\\j&\in\left\{0,1,\cdots,(n/2-1)\right\}\end{aligned}
$$
因为$A(\omega_n^m)$后半部分$A(\omega_n^{m+\frac{n}{2}})$计算完全由前面的$A_0(\omega_\frac{n}{2}^m)$和$A_1(\omega_\frac{n}{2}^m)$来表示，这里计算量才真正得到了减少。

最终FFT输出的是原多项式在$n$个$n$次方根的值。

码位倒序

由于基于FFT算法按时间奇偶抽取的方式改变了原序列的自然序列，这就要求原序列在进入算法之前要将序列调整为符合算法要求的顺序，而新序列与原序列之间满足"码位倒序"，即新序列是原序列每个二进制编号的"反序"。

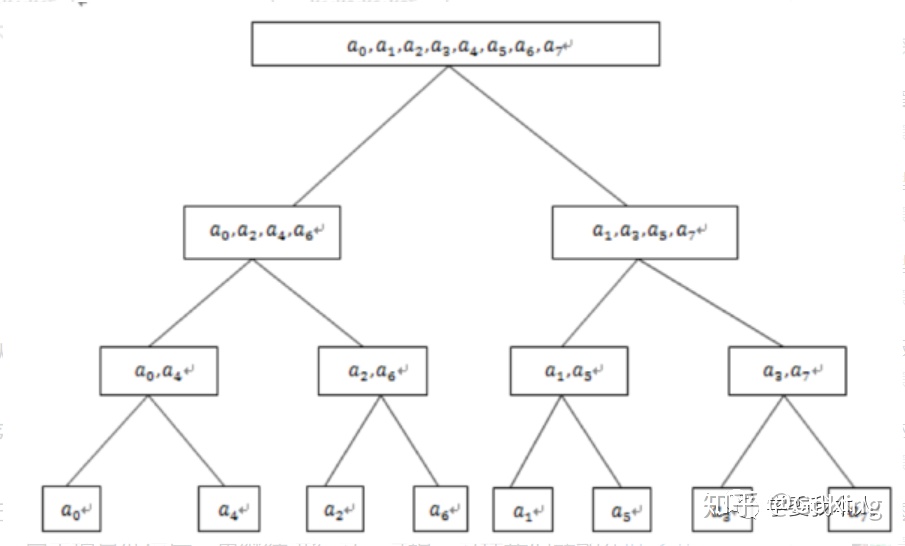
当FFT按时间奇偶抽取时就离不开这个过程，上图就是简单的按时间抽取的过程，可以看到: 当$N=8$时，算法最终进入处理的$a_0\cdots a_8$顺序变为$(a_0,a_4,a_2,a_6,a_1,a_5,a_3,a_7)$, 其下标二进制形式为$000, 100, 010, 110, 001, 101, 111$. (向右进位)

将其下标二进制反序：$000, 001, 010, 011, 100, 101, 110, 111$

所以我们可以通过下标二进制反序求得

code

#define _USE_MATH_DEFINES
#include <bits/stdc++.h>

using namespace std;

int Extend(int num_coef);
void ReverseOrder(int n, float* coefR, float* coefI);
void Input(int num_coef, int n, float* dataR, float* dataI);
void Calculate(int P, int n, int r, int B, float* dataR, float* dataI);
void Print(int n, float* dataR, float* dataI);

int main(int argc, char** argv) {
    cout.setf(ios_base::fixed, ios_base::floatfield);
    cout.setf(ios_base::showpoint);
    cout.precision(5);

    int num_coef;
    cin >> num_coef;
    float *dataR, *dataI;
    int n = Extend(num_coef);

    dataR = new float[n];
    dataI = new float[n];

    Input(num_coef, n, dataR, dataI);

    ReverseOrder(n, dataR, dataI);
    for(int i=0;i<n;i++){
        cout<<dataR[i]<<" ";
    }
    cout<<endl;

    int M = log2(n);
    for (int L = 1; L <= M; L++) {
        int B = pow(2, L - 1);
        for (int j = 0; j <= B-1; j++) {
            int k = pow(2, M - L);
            int P = j * k;
            for (int i = 0; i <= k-1; i++) {
                int r = j + 2 * B * i;
                Calculate(P, n, r, B, dataR, dataI);
            }
        }
    }
    Print(n, dataR, dataI);
    system("pause");
    return 0;
}

int Extend(int num_coef) {
    int m = log2(num_coef);
    if (num_coef == pow(2, m))
        return num_coef;
    else
        return pow(2, m + 1);
}

void Input(int num_coef, int n, float* dataR, float* dataI) {
    cout << "R" << endl;
    for (int i = 0; i < num_coef; i++) {
        cin >> dataR[i];
    }
    cout << "I" << endl;
    for (int i = 0; i < num_coef; i++) {
        cin >> dataI[i];
    }
    if (n > num_coef)
        for (int i = num_coef; i < n; i++) {
            dataR[i] = 0;
            dataI[i] = 0;
        }
}

void ReverseOrder(int n, float* coefR, float* coefI) {
    int m = log2(n);
    int head, rear;
    int a1, an;
    float tempR, tempI;
    for (int i = 0; i < pow(2, m); i++) {
        int j=0;
        for (int k = 0; k < (m + 1) / 2; k++) {
            a1 = 1;
            an = pow(2, m - 1);
            a1 <<= k;
            an >>= k;
            head = i & an;
            rear = i & a1;
            if (0 != head)
                j = a1|j;
            if (0 != rear)
                j = an|j;
        }
        if (i < j) {
            swap(coefR[i], coefR[j]);
            swap(coefI[i], coefI[j]);
        }
    }
}

void Calculate(int P, int n, int r, int B, float* dataR, float* dataI){
    /*进行蝶形运算*/
    //t = W * A1, W = cos(2 * PI * P / n) - i * sin(2 * PI * P / n)
    cout<<M_PI<<endl;
    float tR = dataR[r + B] * cos(2 * M_PI * P / n) + dataI[r + B] * sin(2 * M_PI * P / n);
    float tI = dataI[r + B] * cos(2 * M_PI * P / n) - dataR[r + B] * sin(2 * M_PI * P / n);
    //A(r) = A0 + W * A1
    //A(r + B) = A0 - W * A1
    dataR[r + B] = dataR[r] - tR;
    dataI[r + B] = dataI[r] - tI;
    dataR[r] = dataR[r] + tR;
    dataI[r] = dataI[r] + tI;
}

void Print(int n, float* dataR, float* dataI){
    cout << "result:" << endl;
    for (int i = 0; i < n; i++) {
        if(dataI[i] >= 0)
            cout << dataR[i] << "+" << dataI[i] << "i" << "\t";
        else
            cout << dataR[i] << dataI[i] << "i" << "\t";
    }
    cout << endl;
}

并行FFT

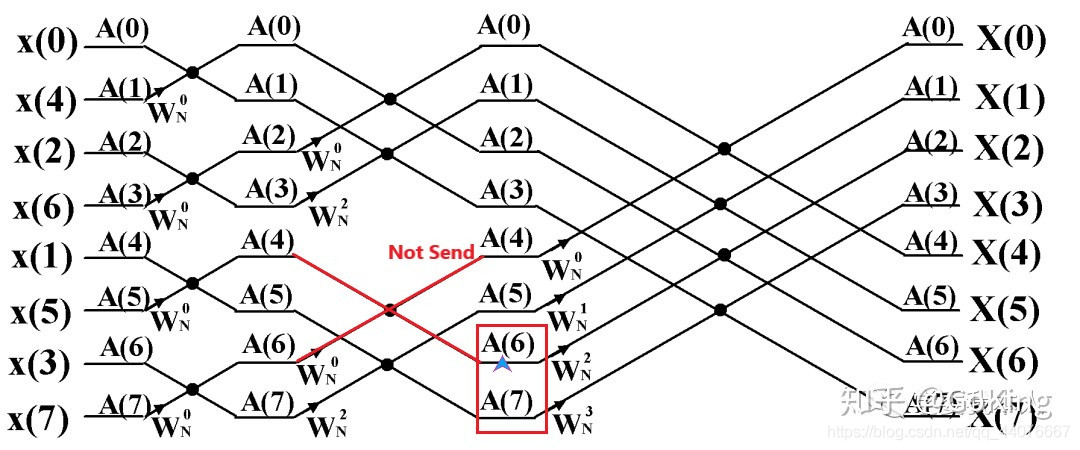
当系数项数$n=8$, 进程数$p=3$时，进程资源进行如下划分：

说明:

在每个进程中用mdataR[]和mdataI[]来存储结果的实部和虚部
在每级蝶形计算前先把上一级的结果广播给每个进程(从其他进程获取数据可能发生死锁)
为被分配的元素由0号进程处理

在进行第L级运算时，遍历mdataR[]. mdataI[]

若是已分配的元素：

若对应鲽形组的上半部分，且鲽形组的下半部分也在此进程中，则直接更新两个元素：
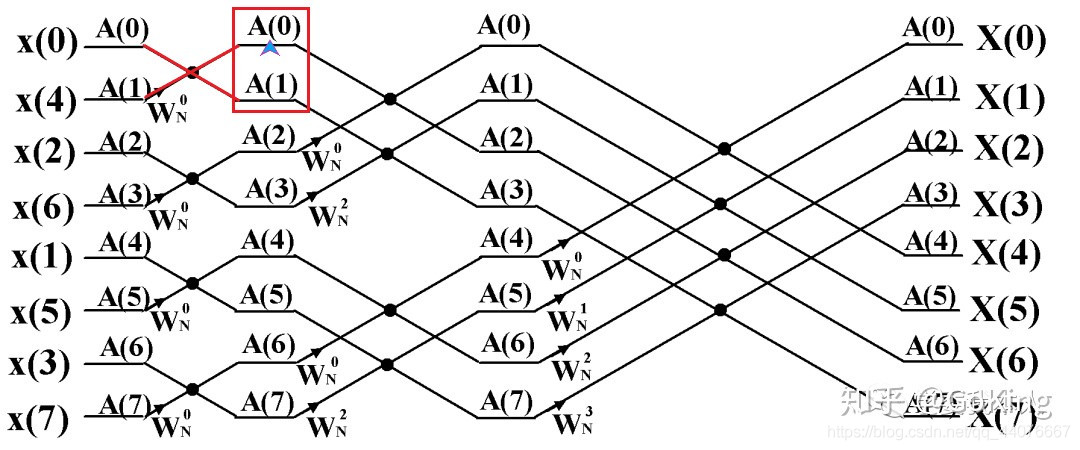
若对应鲽形组的上半部分，且蝶形组的下半部分不在此进程中，对下半部分的元素进行分析：
- 如果是已分配元素：更新当前元素，同时将下半部分对应元素发送给指定进程
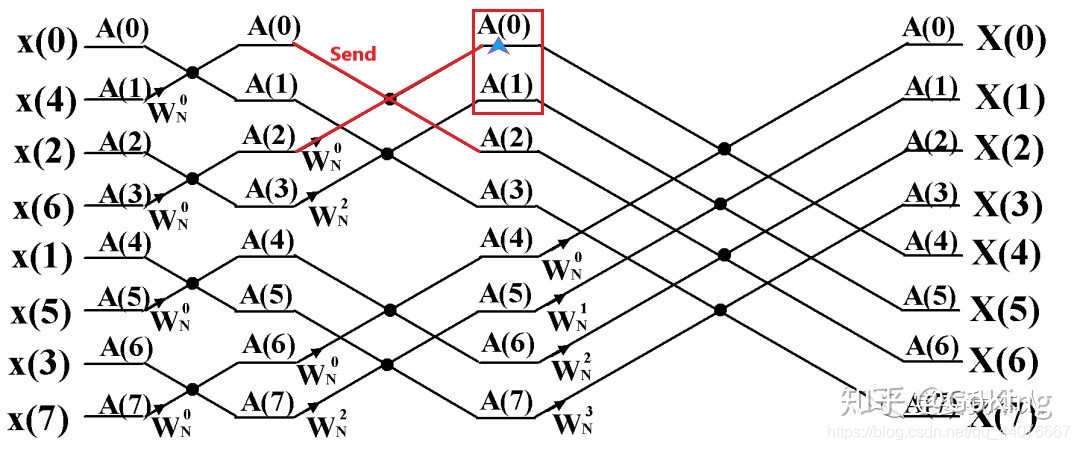
- 如果是未分配的元素：更新当前元素，但是不发送下半部分对应的元素(发送给0号进程可能造成死锁)
注意：这里的发送的数据指的是计算的结果，并非蝶形组左边的数据，还望不要被图片所误导，这样标注仅是为了说明进程间的发送情况。
若是对应蝶形组的下半部分，则接收其他进程发送过来的数据：

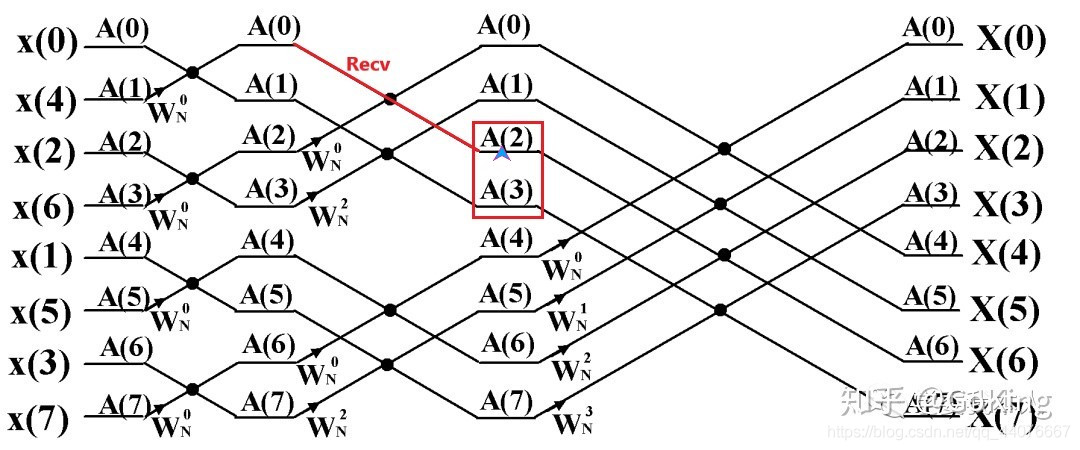
若是未分配元素：

若对应蝶形组的上半部分，则直接更新两个元素：
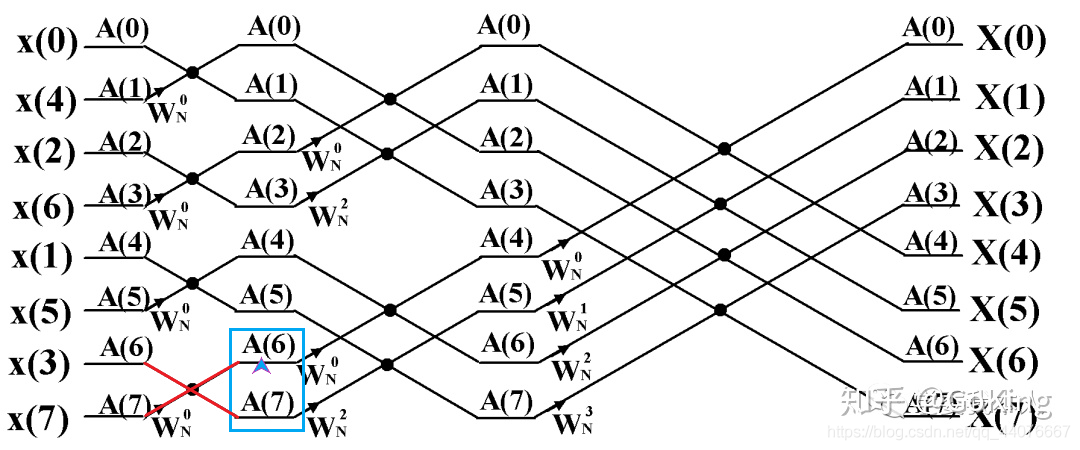
若对应蝶形组的下半部分，则更新此元素：

当M级蝶形计算计算完毕，即可得到结果。

code

#define _USE_MATH_DEFINES
#include <math.h>
#include <mpi.h>
#include <stdlib.h>
#include <algorithm>
#include <iostream>

using namespace std;

int Extend(int num_coef);
void ReverseOrder(int n, float* coefR, float* coefI);
void Input(int num_coef, int n, float* dataR, float* dataI);
void Calculate(int P, int n, int r, int B, float* dataR, float* dataI, float& tempR, float& tempI, float& mdataR, float& mdataI);
void Print(int n, float* dataR, float* dataI);

int main(int argc, char** argv) {
    cout.setf(ios_base::fixed, ios_base::floatfield);
    cout.setf(ios_base::showpoint);
    cout.precision(2);

    int num_coef = atoi(argv[1]);
    float *dataR, *dataI, *mdataR, *mdataI;
    float tempR, tempI;

    int myrank, size;
    MPI_Init(&argc, &argv);
    MPI_Comm_rank(MPI_COMM_WORLD, &myrank);
    MPI_Comm_size(MPI_COMM_WORLD, &size);
    MPI_Status status;

    int n = Extend(num_coef);
    int msize = n / size;
    mdataR = new float[msize];
    mdataI = new float[msize];
    dataR = new float[n];
    dataI = new float[n];

    if (0 == myrank) {
        Input(num_coef, n, dataR, dataI);
        ReverseOrder(n, dataR, dataI);
    }
    MPI_Barrier(MPI_COMM_WORLD);

    int M = log2(n);
    int start = myrank * msize;
    for (int L = 1; L <= M; L++) {
        MPI_Bcast(dataR, n, MPI_FLOAT, 0, MPI_COMM_WORLD);
        MPI_Bcast(dataI, n, MPI_FLOAT, 0, MPI_COMM_WORLD);

        int B = pow(2, L - 1);
        int k = pow(2, M - L);

        for (int j = 0; j < msize; j++) {
            int r = start + j;
            if ((r % (2 * B)) >= B) {
                if (j - B < 0) {
                    MPI_Recv(&mdataR[j], 1, MPI_FLOAT, (r - B) / msize, r, MPI_COMM_WORLD, &status);
                    MPI_Recv(&mdataI[j], 1, MPI_FLOAT, (r - B) / msize, r, MPI_COMM_WORLD, &status);
                }
                continue;
            }

            int P = (r % B) * k;

            Calculate(P, n, r, B, dataR, dataI, tempR, tempI, mdataR[j], mdataI[j]);
            if (j + B + 1 > msize) {
                if (r + B < msize * size) {
                    MPI_Send(&tempR, 1, MPI_FLOAT, (r + B) / msize, r + B, MPI_COMM_WORLD);
                    MPI_Send(&tempI, 1, MPI_FLOAT, (r + B) / msize, r + B, MPI_COMM_WORLD);
                }
            } else {
                mdataR[j + B] = tempR;
                mdataI[j + B] = tempI;
            }
        }

        int remainStartID = msize * size;
        if ((0 == myrank) && (remainStartID != n)) {
            for (int j = 0; j < n - remainStartID; j++) {
                int r = remainStartID + j;
                int P = (r % B) * k;
                if((r%(2*B))>=B){
                    if(j-B<0){
                        float tR = dataR[r] * cos(2 * M_PI * P / n) + dataI[r] * sin(2 * M_PI * P / n);
                        float tI = dataI[r] * cos(2 * M_PI * P / n) - dataR[r] * sin(2 * M_PI * P / n);
                        dataR[r] = dataR[r - B] - tR;
                        dataI[r] = dataI[r - B] - tI;
                    }
                    continue;
                }
                Calculate(P,n,r,B,dataR,dataI,dataR[r+B],dataI[r+B],dataR[r],dataI[r]);
            }
        }
        MPI_Barrier(MPI_COMM_WORLD);
        MPI_Gather(mdataR,msize,MPI_FLOAT,dataR,msize,MPI_FLOAT,0,MPI_COMM_WORLD);
        MPI_Gather(mdataI,msize,MPI_FLOAT,dataI,msize,MPI_FLOAT,0,MPI_COMM_WORLD);

    }
    if(0==myrank){
        Print(n,dataR,dataI);
    }
    MPI_Finalize();
    return 0;
}

int Extend(int num_coef) {
    int m = log2(num_coef);
    if (num_coef == pow(2, m))
        return (num_coef);
    else
        return (pow(2, m + 1));
}

void ReverseOrder(int n, float* coefR, float* coefI) {
    int m = log2(n);
    int head, rear;
    int a1, an;
    for (int i = 0; i < pow(2, m); i++) {
        int j = 0;
        for (int k = 0; k < (m + 1) / 2; k++) {
            a1 = 1;
            an = pow(2, m - 1);
            a1 <<= k;
            an >>= k;
            head = i & an;
            rear = i & a1;
            if (0 != head)
                j = a1 | j;
            if (0 != rear)
                j = an | j;
        }
        if (i < j) {
            swap(coefR[i], coefR[j]);
            swap(coefI[i], coefI[j]);
        }
    }
}

void Input(int num_coef, int n, float* dataR, float* dataI){
    cout << "R: ";
    int i;
    for (int i = 0; i < num_coef; i++) {
        cin >> dataR[i];
    }
    cout << "I: ";
    for (i = 0; i < num_coef; i++) {
        cin >> dataI[i];
    }
    if (n > num_coef)
        for(; i < n; i++){
            dataR[i] = 0;
            dataI[i] = 0;
        }
}

void Calculate(int P, int n, int r, int B, float* dataR, float* dataI, float& tempR, float& tempI, float& mdataR, float& mdataI) {
    /*进行蝶形运算*/
    //t = W * A1, W = cos(2 * PI * P / n) - i * sin(2 * PI * P / n)
    float tR = dataR[r + B] * cos(2 * M_PI * P / n) + dataI[r + B] * sin(2 * M_PI * P / n);
    float tI = dataI[r + B] * cos(2 * M_PI * P / n) - dataR[r + B] * sin(2 * M_PI * P / n);
    //A(r) = A0 + W * A1
    //A(r + B) = A0 - W * A1
    tempR = dataR[r] - tR;
    tempI = dataI[r] - tI;
    mdataR = dataR[r] + tR;
    mdataI = dataI[r] + tI;
}

void Print(int n, float* dataR, float* dataI) {
    cout << "result:" << endl;
    for (int i = 0; i < n; i++) {
        if (dataI[i] >= 0)
            cout << dataR[i] << "+" << dataI[i] << "i"
                 << "\t";
        else
            cout << dataR[i] << dataI[i] << "i"
                 << "\t";
    }
    cout << endl;
}

最后一次更新于2022-03-17

丙乙日寄

问脑哪得清如许，没有源头活水来。

快速傅里叶变换

快速傅里叶变换

准备

多项式的系数表示法

多项式的点值表示

快速傅里叶变换

单位根

FFT

FFT如何减少计算量

蝶形运算

码位倒序

code

并行FFT

code

zotero

牛客小白月赛43