行列式的性质

1. 行列式与他的转置行列式相等，$D=D^T$.
2. 互换行列式的两行(列)，行列式的值变号。
   • 推论：如果行列式D中有两行(列)的元素相同，则$D=0$.
3. 用数$k$乘以行列式的某一行(列),等于用数$k$乘以此行列式.
   • 推论1：如果行列式某一行为的元素为0，则$D=0$.
   • 推论2：如果行列式的两行成比例，则$D=0$.
4. 若行列式的某一行的元素都是两数之和，则行列式可以写成两个行列式的和.
5. 将行列式的某一行的所有元素同乘以数$k$后加到另一行对应的元素上，行列式的值不变.
6. $n$阶行列式$D=|a_{ij}|$等于它的任意一行的各元素预期对应的代数余子式乘积的和，$n$阶行列式$D=|a_{ij}|$的某一行的元素与另一行的对应元素的代数余子式乘积的和等于零.
7. 行列式按某$k$行展开-拉普拉斯定理.设在$n$阶行列式中任意取定了$k$行，则由这$k$行元素组成的一切$k$阶子式与他们各自的代数余子式乘积的和组成的行列式$D$.

---

特殊行列式

• 下三角行列式的值
• 上三角行列式的值
• 对角形行列式的值
• 负对角线行列式的值

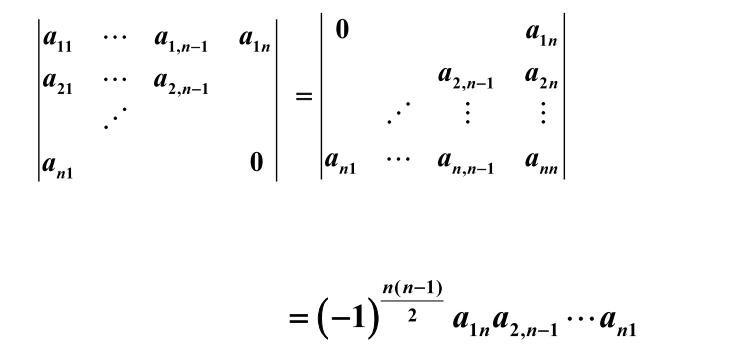
2. 范德蒙(Vandermonde)行列式

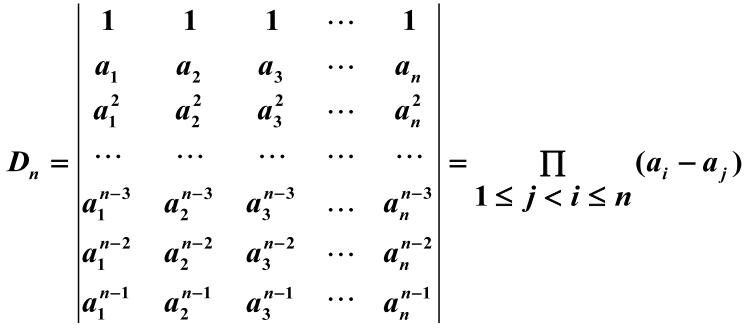
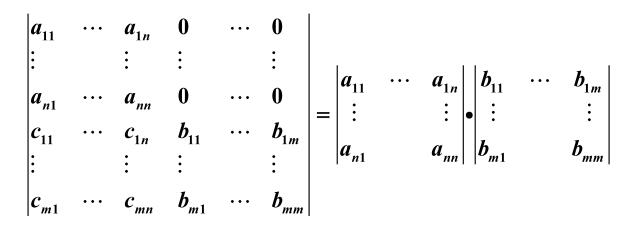
3. 拉普拉斯两个特殊情形

---

Cramer法则

---

例题

行列式的计算

类型一

两条线行列式 (非零元分布在两条线上)

• 按行(列)展开

• 拉普拉斯展开

  类型二

  三条线行列式

• 三对角行列式
  

  按行列展开找递推公式

• 爪型行列式
  

  消去化为上三角

• Hessenberg型行列式
  

  按行列展开找递推公式，可能有$D_n$与$D_{n-1},D_{n-2}$有关

类型三

各行（列）元素之和相等的行列式--行加法（列加法）

各列加到第一列提取公因式

类型四

除主对角元素外其余元素全相等

各行都减第一行，化成爪型行列式。或者进行拆分，找递推式。

类型五

Vandermonde行列式

类型六

其他类型行列式，矩阵行列式求导

---

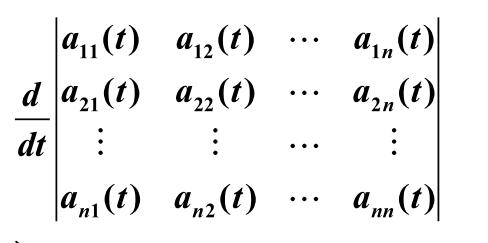
降阶公式

第一降阶公式

设$A$为$n$阶可逆矩阵，$\alpha, \beta$为$n$列向量，则

$$|A+ \alpha \beta^{T}| = |A|( 1+\beta^{T}A^{-1}\alpha)$$

第二降阶公式

设$A$为$n$阶可逆矩阵，$B_1$为$n \times m$矩阵，$B_2$为$m \times n$矩阵

$$|A+B_1B_2|=|A|\cdot|E_m+B_2A^{-1}B_1|$$

第三降阶公式

设$A$为$n$阶矩阵，$\alpha, \beta$为$n$列向量，则

$$|A+\alpha\beta^{T}|=|A|+\beta^{T}A^{*}\alpha| $$